« La résolution de problèmes constitue le critère principal de la maîtrise des connaissances dans tous les domaines des mathématiques, mais elle est également le moyen d’en assurer une appropriation qui en garantit le sens. » BO du 30 juillet 2020.

L’aptitude des élèves à résoudre des problèmes va dépendre principalement de trois facteurs :
• Les connaissances mathématiques des élèves (nombres en jeu, sens des opérations)
• La mémoire des problèmes similaires préalablement résolus
• Des compétences et des aptitudes diverses (confiance, engagement, capacité à lire et comprendre le problème, capacité à organiser et à structurer le travail).

Quels problèmes les élèves de cours moyen doivent-ils savoir résoudre ?

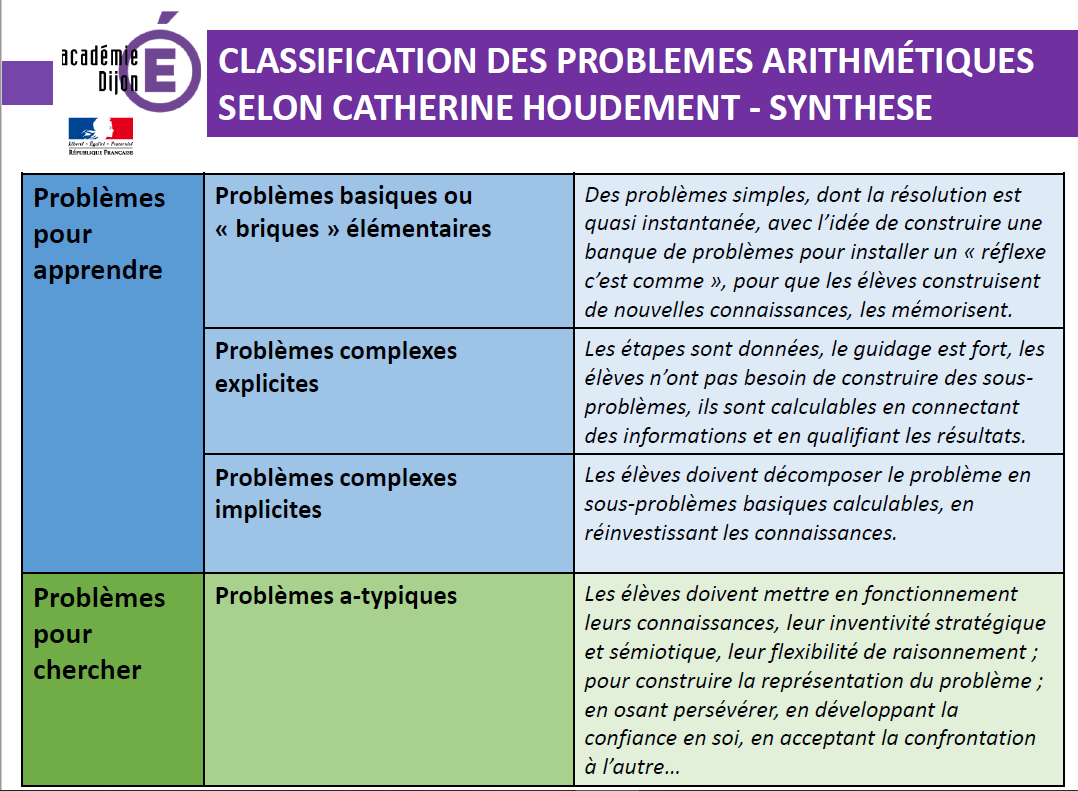
Il n’est bien évidemment pas possible d’établir une liste exhaustive des problèmes que les élèves de cours moyen doivent savoir résoudre. Le guide propose une classification en trois catégories principales qui doit permettre d’aider les professeurs à structurer l’enseignement de la résolution de problèmes dans leur classe avec : — les problèmes en une étape — les problèmes en plusieurs étapes — les problèmes atypiques.
Il existe une catégorie de problèmes particuliers, mentionnée explicitement dans le programme de cycle 3 : les problèmes de proportionnalité.

Que faire quand un élève n’arrive pas à résoudre un problème ?
Quand un élève donne une résolution erronée, la première action du professeur doit être d’analyser la production de l’élève pour repérer la ou les difficultés rencontrées. Cette analyse peut s’appuyer sur le modèle de résolution en quatre phases (comprendre, modéliser, calculer, répondre).

Il est généralement difficile de distinguer si les difficultés relèvent de la phase « comprendre » ou de la phase « modéliser » à partir des seules traces écrites ; un échange avec l’élève est alors nécessaire.

Il est possible d’agir sur trois curseurs en fonction de l’objectif visé : — la structure du problème ; — le texte du problème ; — le champ numérique.

Doit-on apprendre aux élèves à faire des schémas ?

À quel moment doit-on introduire les schémas en barres ?

La compétence « représenter » fait partie des compétences que les élèves doivent développer à l’école élémentaire. Les schémas sont souvent indispensables aux élèves pour pouvoir modéliser correctement les problèmes qui leur sont soumis. Quatre types de schémas devant être connus des élèves de cours moyen : les schémas en barres, les schémas proposant un déplacement sur une droite numérique, les tableaux, les arbres. Les schémas en barres sont traditionnellement introduits progressivement à partir du CE1. Ce qui est particulièrement important pour les schémas en barres comme pour les autres outils de représentation, c’est de conserver une certaine cohérence d’utilisation d’année en année, tout au long de la scolarité obligatoire, afin de permettre aux élèves de garder les mêmes repères et de devenir de plus en plus efficaces en résolution de problèmes.

• Pour résoudre des problèmes, les enfants comme les adultes s’appuient en priorité sur leur mémoire de problèmes résolus.

Qu’est-ce que résoudre un problème ?

Il y a quatre phases fondamentales pour la résolution de problèmes : comprendre, modéliser, calculer et répondre, modèle simplifié fortement inspiré du modèle de Lieven Verschaffel et d’Erik De Corte :

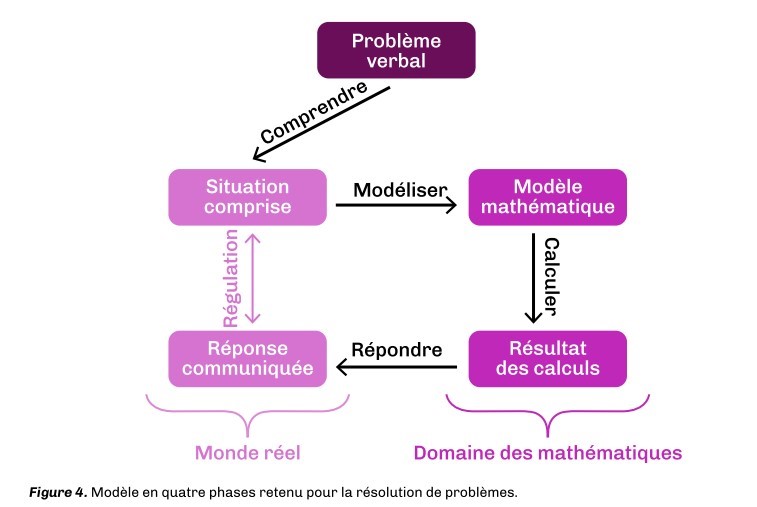
Comprendre

• Un problème est en premier lieu une histoire qu’il va falloir comprendre. La compréhension doit être fine.
• Il y a une question : qu’est-ce que l’on cherche ?

Modéliser

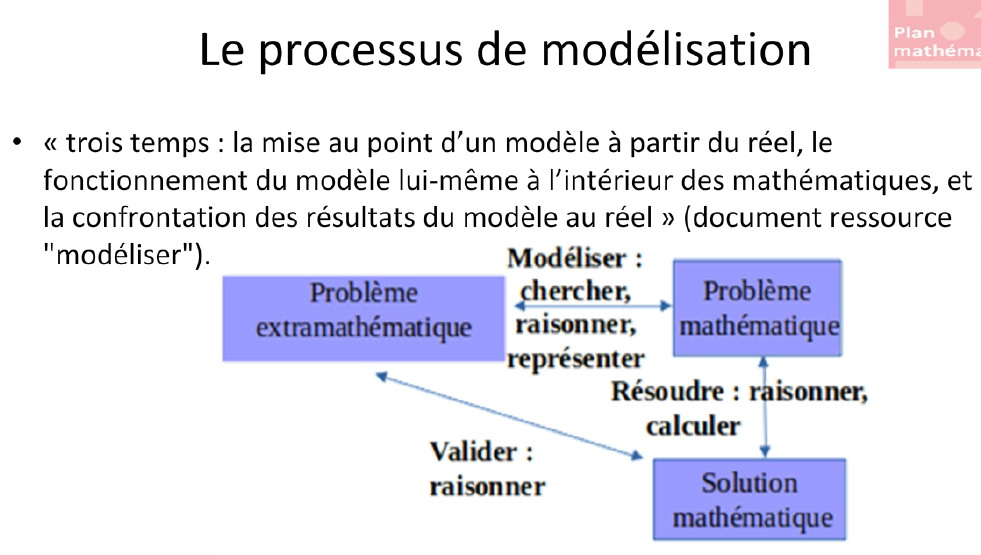
• La modélisation est le « processus par lequel l’individu convertit les données des situations réelles en problème mathématique ».
• De façon générale, quatre des « six compétences majeures de l’activité mathématique » (chercher, modéliser, représenter, calculer, raisonner et communiquer) mises en exergue dans les programmes des cycles 2, 3 et 4 sont mobilisées lors du passage de la situation comprise à partir de l’énoncé au modèle mathématique retenu pour résoudre le problème.
  Calculer
• Ces calculs peuvent être réalisés soit mentalement, soit en ligne, soit en posant les opérations.
• La résolution de problèmes va contribuer à renforcer la bonne maîtrise des techniques de calculs attendues des élèves (calcul mental ou calcul posé).
  Répondre :
• Lors de l’enseignement de la résolution de problèmes à l’école élémentaire, cette phase « répondre » est souvent réduite à la demande d’écriture d’une phrase respectant les canons usuels (une phrase complète, qui commence par une majuscule et qui finit par un point, comprenant le nombre solution associé à son unité).
  Identifier les obstacles à la résolution de problèmes pour les élèves
  Plusieurs éléments du texte de l’énoncé peuvent ainsi constituer des obstacles à cette bonne compréhension :
• Le degré de familiarité de l’élève avec l’environnement du problème : familiarité avec le contexte, familiarité avec le lexique lié à ce contexte, etc…
  Il pourra souvent être intéressant de créer des problèmes directement en lien avec les activités des élèves et les événements vécus par la classe : activités pratiquées dans le cadre de l’EPS, sorties organisées, activités menées en sciences, etc.
• La longueur et la forme de l’énoncé : les textes peuvent devenir plus longs au cours moyen et les informations à prélever plus nombreuses.
  Il est important de confronter les élèves dès le début du cours moyen à des énoncés de problèmes de plus de deux ou trois lignes sans complexité particulière au-delà de la longueur, afin de leur apprendre à ne pas être déstabilisés par de tels énoncés et à structurer les données pour pouvoir répondre à la question posée.
• Le lexique spécifique aux mathématiques
  Les difficultés liées au lexique nécessitent une grande vigilance du professeur lors du choix des problèmes. Un temps de résolution de problèmes ne doit pas être vu comme une opportunité de faire acquérir de nouveaux mots aux élèves. Certaines séances de résolution de problèmes commencent parfois par de longues explications sur le texte de l’énoncé et le lexique qu’il contient.
  Cette pratique est généralement à éviter, car elle éloigne les élèves de l’objectif visé par les séances de résolution de problèmes. Elle est particulièrement ennuyeuse pour les élèves qui ont souvent perdu toute motivation à résoudre le problème.
• Des mots-clés de l’énoncé concordants ou non avec la modélisation : présence de mots comme « plus », « perdre », « fois », « partager » qui incitent fortement à effectuer une opération en particulier ;
• Un scénario, évoqué par l’énoncé, facilitant ou non la perception des relations mathématiques en jeu : relations entre les entités présentes dans l’énoncé, relations décrites au sein de l’énoncé ou à construire par l’élève, etc. ;
• L’inscription ou non dans le champ de validité de la conception intuitive des opérations : par exemple des problèmes de gains pour lesquels il faut effectuer une soustraction ne sont pas inscrits dans ce champ de validité ;
• La présence de données inutiles
  Proposer des problèmes avec des données inutiles est particulièrement intéressant pour repérer des difficultés d’élèves qui risqueraient de ne pas être décelées lors du traitement d’un problème en une étape avec deux données numériques.
  Cependant, il ne s’agit pas d’en faire une tâche technique, qui consisterait à repérer les données utiles et inutiles dans des énoncés de problèmes. En résolution de problèmes, la tâche dévolue aux élèves doit rester de résoudre des problèmes.
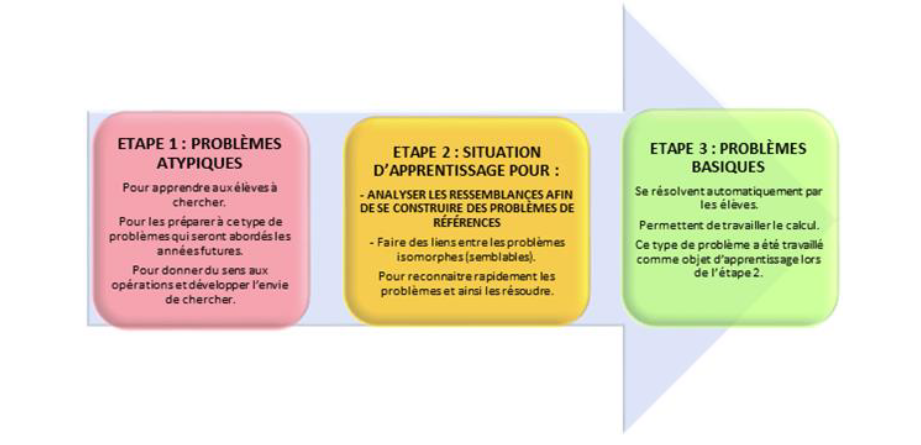
  Comment délivrer un enseignement structuré de la résolution de problèmes ?
  Construire un enseignement de la résolution de problèmes est complexe, car il faut mener de front des actions dans deux directions qui peuvent sembler difficiles à concilier :
  — faire acquérir aux élèves des stratégies efficaces de résolution de problèmes, adaptées à des formes de problèmes bien identifiées rencontrées au cours moyen, et des quasi-automatismes permettant de mobiliser aisément et à bon escient ces stratégies en s’appuyant sur la mémoire des problèmes résolus précédemment ;
  — apprendre aux élèves à ne pas être déstabilisés par des problèmes nouveaux, non rencontrés précédemment, et développer chez eux des habilités en résolution de problèmes.
  Une fois que l’enseignant a explicité les connaissances ou savoir-faire utiles, les élèves doivent pouvoir les mettre en œuvre dans de nouveaux problèmes, l’utilisation d’un cahier étant cette fois indispensable pour laisser des traces pour l’enseignant et pour l’élève.

• S’appuyer sur l’institutionnalisation : une trace écrite sous forme d’affichage permet un accès immédiat et rapide en classe et donne l’occasion de faire des analogies entre des problèmes qui n’ont aucun trait de surface commun : « Ce problème, c’est comme… ». Ces analogies sont essentielles.
• Une trace écrite dans le cahier est également incontournable et nécessaire.
• S’appuyer sur l’évaluation pour renforcer les apprentissages : l’effet positif sur les apprentissages de petites évaluations courtes mais fréquentes a été clairement mis en lumière par des travaux de recherche. Ces évaluations courtes, sous la forme d’un unique problème, permettent aux élèves de renforcer leur attention sur des outils particuliers ou des stratégies qui leur ont été enseignées.

150 pages, parution sur EDUSCOL en janvier 2022

Téléchargeable : https://eduscol.education.fr/251/mathematiques-cLisacle-3

Langage oral, plurilinguisme et résolution de problèmes

L’entretien d’explicitation dans le cas de la résolution de problèmes

Une proposition d’interaction en relation duelle PE/E

• Entretien individuel ou immédiatement après la réalisation du problème, d’une durée adaptée aux capacités attentionnelles de l’élève.
• Laisser le temps à l’élève de formuler, d’indiquer sa procédure de résolution, et d’exprimer sa pensée.
• Intégrer les réponses de l’élève dans son ajustement pédagogique, sans monopoliser la parole.
• Formuler des questions de manière positive : ce que l’élève peut faire, comment s’y prendre.
• Lors des séquences didactiques, prendre en compte la réalité macro et micro-sociolinguistique des élèves afin de l’utiliser pour les apprentissages langagiers en mathématiques.
  Lors de la mise en train, l’activité va prendre du sens en s’ancrant dans la vie de la classe, en permettant l’émergence des représentations et des connaissances des élèves sur la thématique proposée.
  Tout ceci favorisera un espace d’interactions plurilingues, dans lequel les élèves se déplacent en modifiant, à travers la permissivité linguistique institutionnalisée, leurs rapports à l’objet d’apprentissage.
  Au cours des séquences didactiques d’enseignement / apprentissage sont organisées assez classiquement en trois phases :
• La mise en situation
• La situation-recherche
• La synthèse et d’institutionnalisation, le français restera la langue de référence.
• La synthèse, au cours de laquelle le français restera la langue de référence et servira notamment au partage des observations, des comparaisons et pour la découverte de règles. Loin de « parasiter ou de retarder le travail proprement dit sur la langue cible, la réflexion et l’analyse consciente, par exemple, de fonctionnements d’autres systèmes comparés à ceux de la langue maternelle vont favoriser la distanciation par rapport au code pour mieux se l’approprier. Moore, 1995
• Lors de la mise en train, l’activité va prendre du sens en s’ancrant dans la vie de la classe, en permettant l’émergence des représentations et des connaissances des élèves sur la thématique proposée. Un espace nouveau d’interactions plurilingues se développe, dans lequel les élèves se déplacent en modifiant, à travers la permissivité linguistique institutionnalisée, leurs rapports à l’objet d’apprentissage.
• Au cours de la situation-recherche, les élèves vont s’approprier de nouvelles connaissances, recourant à différentes procédures « pour organiser et analyser des données langagières, pour manipuler les formes du langage, pour trouver des éléments de règles de fonctionnement, etc. ». (Perregaux, de Goumoëns, Jeannot& de Pietro, 2003, p. 31).
• Dans un entrainement métalinguistique souvent intensif et Perdereau-Bilski,(2000) considère que les situations problèmes proposées aux élèves dans le cadre d’activités d’Eveil aux langues, les ont entrainés dans un travail « de réflexion sur la langue, de mise à l’épreuve des variations langagières d’une langue à une autre par la découverte de points communs et de différences. »
  Les outils numériques :
• L’outil numérique « le visualiseur » contribuent à améliorer et à optimiser les temps de mise en commun tout en permettant aux élèves de verbaliser et d’expliciter les stratégies mises en œuvre lors de la résolution du problème. Ils pourront ainsi expliciter leurs stratégies à toute la classe, grâce au vidéo projecteur.
• L’outil numérique « le vidéo projecteur » permet de traiter un nombre important de problèmes en un temps très court. Ce traitement de nombreux problèmes avec les mêmes données numériques permet une focalisation renforcée sur la compréhension de l’énoncé (histoire et question) et la modélisation de la situation. La régulation entre chaque problème permet de rendre explicites les stratégies utilisées par les élèves. La présentation avec le vidéo projecteur en un temps de résolution limitée permet une concentration plus renforcée des élèves sur la tâche proposée.

Article réalisé par : Mmes Christine HO YORCK KRUI et Cindy COPHY